Intervenant·es et résumés

Arnaud Duval - L'analyse isogéométrique pour l'optimisation de forme

L'analyse isogéométrique (IGA), apparue au début des année 2000, peut être considérée comme une extension de la méthode des éléments finis. Elle se démarque en utilisant des fonctions issues de la conception assistée par ordinateur (les B-splines et leurs variantes) pour approximer la solution du problème à résoudre. De ce fait, elle constitue un lien fort entre la CAO et le calcul de structures.

Ce lien permet de traiter efficacement des cas d'optimisation de forme pour les problèmes de mécanique auto-adjoints (élasticité linéaire avec des fonctionnelles faisant intervenir volume, souplesse, contrainte, déplacement et dont les variables de design sont directement liées à la positions des points de contrôle d'une géométrie décrite par des B-splines). L’optimisation fait appel à deux modèles intrinsèquement liés par un opérateur de raffinement : un modèle géométrique qui décrit la forme à optimiser via des variables de design et un modèle sur lequel l'analyse mécanique est conduite. Dans le cas d'une optimisation via une méthode numérique à gradients, ces derniers peuvent être évaluée directement, ce qui rend le processus numériquement plus efficace qu'en les calculant via des différences finies.

Le cours et le TP auront pour objectif de décrire un modèle géométrique via des B-Splines, de conduire une analyse mécanique en IGA et de résoudre un problème d'optimisation de forme en liant le modèle géométrique et le modèle d'analyse. Le travail sera basé sur le logiciel libre YETI, développé au sein du LaMCoS.

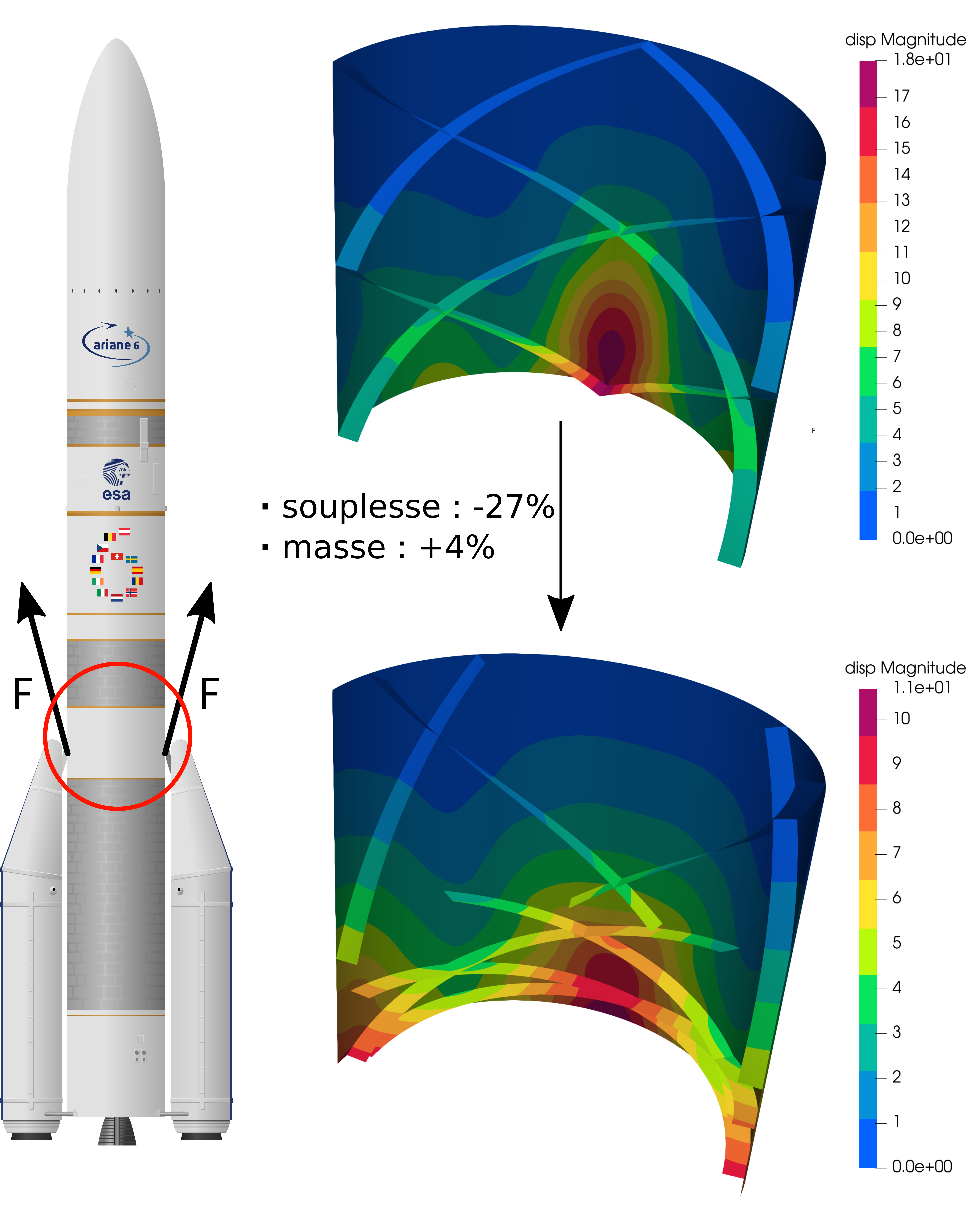
Exemple d'optimisation de forme utilisant l'analyse isogéométrique : placement de raidisseurs sur un tronçon du lanceur Ariane 6 (image lanceur : SkywalkerPL, CC BY 3.0 https://creativecommons.org/licenses/by/3.0, via Wikimedia Commons)

Jérome Gurhem  (ANEO) - ArmoniK: un orchestrateur de calculs open source 

ArmoniK est un logiciel open-source développé par ANEO, conçu pour faciliter le développement d'applications HPC complexes sur des clouds hybrides. ArmoniK est conçu pour y déléguer l'orchestration des calculs et du transfert et propose une programmation basée sur les tâches, disponible pour tout algorithme distribués complexes. ArmoniK assure le passage à l'échelle automatique, sur tout cloud privé ou public et pour tout type de ressources : CPU, GPU, TPU, QPU. Grâce à ArmoniK, la conception d'algorithme complexes se fait de manière évolutive et en mutualisant les serveurs sur site, débordant dans le cloud et améliorant l'empreinte carbone.

Afin de préparer au mieux l'atelier pratique, installez ArmoniK en suivant les pas suivants:

• Cloner le repository github: 
  
  git clone https://github.com/aneoconsulting/ArmoniK.git
  
  
• Installer les preréquis:
  
  
• chmod +x ./infrastructure/utils/scripts/installation/prerequisites-installer.sh
  chmod +x ./infrastructure/utils/scripts/installation/prerequisites/*
  ./infrastructure/utils/scripts/installation/prerequisites-installer.sh

• Compile ArmoniK:
  
  cd ./infrastructure/quick-deploy/localhost
  make

Bernard Yanou et Florent Loete  - Atelier d'Initiation à la Valorisation de la recherche

Quel est le potentiel de valorisation de vos travaux ?

Quand ? Le Mercredi 14 mai APM de 14h à 17h

Qui ? Ouvert à 50 participants sur inscription

Quoi ? Vous êtes étudiant, doctorant ou jeune chercheur en mécanique ? Vous améliorez des modèles scientifiques, perfectionnez des méthodes d’analyse, mettez au point des dispositifs expérimentaux, augmentez la précision ou répétabilité d’une mesure ou d’un phénomène, répondez par une technique adaptée à un « cas d’usage industriel » ? Et vous vous demandez si vos avancées pourraient avoir de la valeur… au-delà des publications scientifiques (indispensables) ?

Venez participer à cet atelier d’initiation à la valorisation des travaux issus de la recherche publique.

Dans un premier temps (séance plénière), nous exposerons la logique et les principes de la valorisation dans le cadre d'une thèse de doctorat. Nous aborderons les bonnes questions à se poser si on veut démarrer un processus de valorisation en parallèle de la thèse.

Dans un second temps (plusieurs ateliers), vous établirez le potentiel de valorisation de votre propre projet en partant de votre sujet de thèse (votre technologie différenciante) ou d’une de problème à résoudre en réfléchissant progressivement à :

• Le bilan de votre technologie différenciante (outil fiche technologique),
• L'analyse de votre Propriété Intellectuelle,
• Le choix du bon secteur socio-économique relativement à la promesse de valeur dans ce secteur et la taille du marché,
• L’établissement du réseau de valeur, le ciblage des clients, de leurs besoins, le croisement (produits) x (segments de client), la liste des briques technologiques,
• Tentative de feuille de route technologique (livraison des briques), de marché (lancement des produits), ainsi que de votre projet de valorisation (vente de licence d’exploitation ou création de start-up ?).

Qui sommes-nous ?

Bernard YANNOU est Professeur des Université en conception de systèmes complexes à CentraleSupélec (Université Paris-Saclay), et Directeur-adjoint de la recherche à CentraleSupélec, en charge de la cellule valorisation des projets des chercheurs et doctorants. Il est également responsable pédagogique du Parcours Entrepreneuriat Deeptech de la Maison du Doctorat de l’Université Paris-Saclay.

Florent LOETE est Docteur et Ingénieur de Recherche, au sein du laboratoire GeePS de CentraleSupélec, ainsi que chargé de valorisation et de maturation au sein de la cellule valorisation de la Direction de la Recherche. Il porte lui-même un projet de maturation technologique dans l’objectif de la création prochaine de la start-up Neo Sense.